Discrete Global Grid System (DGGS) have been proposed as a new geospatial technology and Earth reference system which utilizes a spherical tessellation of space to represent the Earth’s surface and is global in scope. The DGGS framework offers a discrete way for spatial referencing, using cells as the smallest unit of its base rather than coordinates taken from underlying continuous space as used in conventional coordinate systems such as geographic coordinate system (GCS). Each cell’s location is fixed and associated with a specific area. The cells are organized at multiple scales or resolutions and with different cell sizes. It consists of a series of increasingly finer resolution grids as the number of cells monotonically increases with scale and organized in the form of a hierarchy. The resolution of the DGGS is predefined and determined by the subdivision of cells from larger cells into smaller ones. In addition to their equal cell size properties, they also provide several cell typologies for representing data and performing spatial analysis. The DGGS framework also provide a spatial structure for integrating different types and formats of data such as raster and vector in one consistent geospatial model.

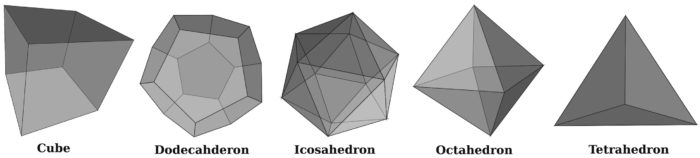
DGGS can be constructed by specifying design elements such as base polyhedron, cell type, refinement, orientation, projection, and cell indexing. Base polyhedrons or Platonic solids are used to represent the spherical approximation of the Earth surface. There are five Platonic solids (cube, dodecahedron, icosahedron, octahedron, and tetrahedron) that are defined on three- dimensional solid geometric spaces formed with one kind of a regular polygon type. The base polyhedron provides the initial spherical domain for representing the DGGS framework. The icosahedron is a preferred choice for DGGS implementations because of its smaller faces and better approximation of the Earth.

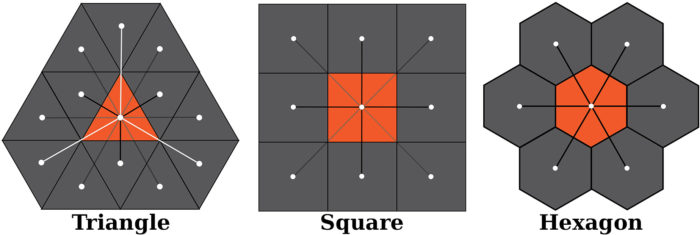
Five base polyhedron for implementing discrete global grid systems (DGGSs).

Cells are the smallest unit of a DGGS framework and can be considered as spherical polygons used to tessellate the surface of the Earth. Three cell types are commonly used in DGGS (squares, triangles, and hexagons) with each having its own merits and disadvantages. For example, squares are congruent, compatible with two-dimensional coordinate systems as well as current GIS software and data formats. However, their typology is not directly compatible with some polyhedrons. Triangles are easy to utilize and render and are compatible with most Platonic solids and provide an efficient geometric connectivity for interpolation of values when used to represent spatial data such as elevation models. They however have complex geometric properties such as complicated cell adjacency relationship and non-uniform orientation. Hexagonal cells have also received much attention due to its properties and advantages. Among the three regular cells, hexagons are the most compact, and quantize the plane with the least average error. Hexagonal lattices can also be used to approximate circular region and offer uniform neighbouring relationships; a property which is desirable for spatial analysis. Hexagons are however non-congruent and larger hexagons cannot be refined into smaller hexagons that perfectly fit within the boundary of the larger one.

Geometric properties and neighbourhood relationships foe triangle, square, and hexagon.

Refinement techniques are used to subdivide the initial polyhedron cells into a set of finer cells in a hierarchical and recursive manner. The ratio of the areas of cells at two different spatial resolutions is termed aperture. DGGS aperture can differ based on cell type and application. In hexagonal DGGS implementation, apertures 3, 4, and 7 are generally used. The geometry and location of cells are the key principle of a DGGS. The location and spatial component of cells in a DGGS framework are represented using unique identifiers which helps to simplify spatial operations and queries.

Hexagonal hierarchical partitioning methods based on aperture 3, aperture 4, and aperture 7.

Representing geospatial features in DGGS

Different spatial data formats can be represented in DGGS as cells or multi cells. To transform and represent point data in DGGS, the point’s geographic coordinate is converted into the DGGS cell it falls into at the specified level. Each cell has a unique identifier at each level, and the position of the cell centroid represents the cell’s geographical coordinates. After generation, duplicate cells are removed where two or more points fall in the same DGGS cell. During DGGS construction, attribute data from the original point feature are extracted to each cell to be used for further spatial analysis or visualization. The geographic coordinates for each DGGS cell’s vertices can also be retrieved to convert cells into polygon features for visualization.

Representation of polygon, polyline, and point spatial data in DGGS model.

Polylines and polygons can be represented in a similar approach. Line features are converted as a sequence of DGGS cells where the original lines traverses grid cell. Polygons can also be modelled as a series of cells contained within the boundary of the original polygon feature. A series of cells can be used to represent a polygon and different polygons can be distinguished using their cell attributes. For raster data, DGGS points are generated covering the extent of the dataset. Subsequently, the raster values are extracted at each cells’ centroid. Raster values can be represented in several ways based on the nature of the data. For categorical datasets such as land-use/land-cover, nearest neighbour or majority techniques are more appropriate. Elevation and climate data can be represented using the average raster values whereas the sum is more suitable when working with population datasets.

Representation of global land-cover, bathymetry, and submarine cable networks with hexagonal DGGS cells.

Works cited

Peterson, P. R. (2017). Discrete Global Grid Systems. In International Encyclopedia of Geography, (Eds.) D. Richardson, N. Castree, M.F. Goodchild, A. Kobayashi, W. Liu, & R.A. Marston,(pp. 1-10).

Robertson, C., Chaudhuri, C., Hojati, M., & Roberts, S. A. (2020). An integrated environmental analytics system (IDEAS) based on a DGGS. ISPRS Journal of Photogrammetry and Remote Sensing, 162, 214-228. doi:10.1016/j.isprsjprs.2020.02.009

Sahr, K., White, D., & Kimerling, A. J. (2003). Geodesic discrete global grid systems. Cartography and Geographic Information Science, 30, 121-134. doi:10.1559/152304003100011090